domingo, 21 de octubre de 2018
miércoles, 17 de octubre de 2018
¡¡Música , matemático!!
Sucesión de Fibonacci en la quinta sinfonía de Beethoven .
LA QUINTA SINFONÍA
La quinta sinfonía de Beethoven es una de las sinfonías más populares en el mundo de la música y también una obra que afamó a su compositor (Ludwig van Beethoven 1770-1827) la fama de esta obra ha llegado hasta nuestros días y se ha convertido en una de esas "piezas clásicas " que no caerán en el olvido.
Compuso otras sinfonías como la tercera , la novena o la décima.
LA SUCESIÓN DE FIBONACCI
LA QUINTA SINFONÍA
La quinta sinfonía de Beethoven es una de las sinfonías más populares en el mundo de la música y también una obra que afamó a su compositor (Ludwig van Beethoven 1770-1827) la fama de esta obra ha llegado hasta nuestros días y se ha convertido en una de esas "piezas clásicas " que no caerán en el olvido.
Compuso otras sinfonías como la tercera , la novena o la décima.
LA SUCESIÓN DE FIBONACCI
Leonardo de Pisa, más conocido como
Fibonacci enunció en 1228 el siguiente problema:
"Alguien puso en un corral una pareja
de conejos recién nacidos con el propósito de averiguar cuántas parejas
habrá al cabo de un año. La prolífica naturaleza de estos animalitos indica que
cada pareja recién nacida requiere un mes de maduración, durante el cual
no se reproduce, pero al finalizar el segundo mes da a luz una
nueva pareja, y luego sigue pariendo cada mes otra pareja. ¿Cuántas
parejas habrá al término de un año, suponiendo que ningún conejo muere en
esta feliz experiencia?"
La solución es la siguiente: al empezar
tenemos una pareja. Al finalizar el primer mes seguimos con una sola pareja. Al
término del segundo mes, el corral ya cuenta con 2 parejas. Al cabo del tercer
mes la pareja inicial da a luz otra pareja: ya hay 3 parejas una nueva. Al
final del cuarto mes, procrea la pareja inicial y la primogénita: tenemos
5 parejas. Al final del quinto mes: 8 parejas y así sucesivamente. Al
culminar el año (12 meses) el corral tendrá 233 parejas de conejos.
El número de parejas de conejos cada
mes corresponde a la siguiente sucesión:1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, 144, 293, ...
Fibonacci también se puede representar como número áureo , que lo podemos encontrar desde en cuadrículas en cámaras de fotos ,en edificios o incluso en instrumentos como el violín o la guitarra eléctrica.
FIBONACCI EN LA QUINTA SINFONÍA
Beethoven parece utilizar los números de Fibonacci en el tema de la 5ª Sinfonía y también en el trascurso de la obra. Aparece el acto principal en los compases 1, 5, 14, 23... Se utilizan mucho los intervalos de 2m (1), 2M (2), 3m (3), 4J (5) i 6m (8).
El clímax de la obra se
encuentra en el 61’8%.
Pero Beethoven no fue el único en utilizar este método en sus obras otros famosos compositores como Bach o Mozart también lo utilizaron.
La mayoría de estudios prueban que estos hechos son casuales y que ninguno de ellos utilizó la razón áurea de forma intencionada... Pero quién sabe , quizá las mates están mas cerca de las artes de lo que yo creo....
QUINTA SINFONÍA VÍDEO
Suscribirse a:
Entradas (Atom)
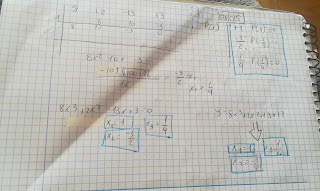
Global examen para casa.
Con dos días he logrado sacar más o menos el examen para casa, me da a mi que con muchos fallos sobre todo la parte dos que para mi era l...
-
Con dos días he logrado sacar más o menos el examen para casa, me da a mi que con muchos fallos sobre todo la parte dos que para mi era l... -
Gerolamo Cardano , o Girolamo Cardano ( 24 de septiembre de 1501 - 21 de septiembre de 1576 ) Fue un médico , además de un m...
-
Abraham de Moivre. Nació el 26 de mayo de 1667 en Vitry-le-François , Champagne (Francia). Aunque su padre er...
